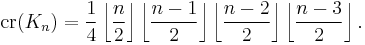Albertson conjecture

In combinatorial mathematics, the Albertson conjecture is an unproven relationship between the crossing number and the chromatic number of a graph. It is named after Michael O. Albertson, a professor at Smith College, who stated it as a conjecture in 2007;[1] it is one of many conjectures made by Albertson in graph coloring theory.[2] The conjecture states that, among all graphs requiring n colors, the complete graph Kn is the one with the smallest crossing number. Equivalently, if a graph can be drawn with fewer crossings than Kn, then, according to the conjecture, it may be colored with fewer than n colors.

It is straightforward to show that graphs with bounded crossing number have bounded chromatic number: one may assign distinct colors to the endpoints of all crossing edges and then 4-color the remaining planar graph. Albertson's conjecture replaces this qualitative relationship between crossing number and coloring by a more precise quantitative relationship. Specifically, a different conjecture of Richard K. Guy (1972) states that the crossing number of the complete graph Kn is

\textrm{cr}(K_n)=\frac14\left\lfloor\frac{n}{2}\right\rfloor\left\lfloor\frac{n-1}{2}\right\rfloor\left\lfloor\frac{n-2}{2}\right\rfloor\left\lfloor\frac{n-3}{2}\right\rfloor.

It is known how to draw complete graphs with this many crossings, by placing the vertices in two concentric circles; what is unknown is whether there exists a better drawing with fewer crossings. Therefore, a strengthened formulation of the Albertson conjecture is that every n-chromatic graph has crossing number at least as large as the right hand side of this formula.[3] This strengthened conjecture would be true if and only if both Guy's conjecture and the Albertson conjecture are true.

The Albertson conjecture is vacuously true for n ≤ 4: K4 has crossing number zero, and all graphs have crossing number greater than or equal to zero. The case n = 5 of Albertson's conjecture is equivalent to the four color theorem, that any planar graph can be colored with four or fewer colors, for the only graphs requiring fewer crossings than the one crossing of K5 are the planar graphs, and the conjecture implies that these should all be at most 4-chromatic. Through the efforts of several groups of authors the conjecture is now known to hold for all n ≤ 16.[4]

There is also a connection to the Hadwiger conjecture, an important open problem in combinatorics concerning the relationship between chromatic number and the existence of large cliques as minors in a graph.[5] A variant of the Hadwiger conjecture, stated by György Hajós, is that every n-chromatic graph contains a subdivision of Kn; if this were true, the Albertson conjecture would follow, because the crossing number of the whole graph is at least as large as the crossing number of any of its subdivisions. However, counterexamples to the Hajós conjecture are now known,[6] so this connection does not provide an avenue for proof of the Albertson conjecture.

Notes

  1. ^ According to Albertson, Cranston & Fox (2009), the conjecture was made by Albertson at a special session of the American Mathematical Society in Chicago, held in October 2007.
  2. ^ Hutchinson, Joan P. (June 19, 2009), In memory of Michael O. Albertson, 1946–2009: a collection of his outstanding conjectures and questions in graph theory, SIAM Activity group on Discrete Mathematics, http://orion.math.iastate.edu/rymartin/dm-net/MOASIAM.pdf .
  3. ^ Albertson, Cranston & Fox (2009).
  4. ^ Oporowski & Zhao (2009); Albertson, Cranston & Fox (2009); Barát & Tóth (2010).
  5. ^ Barát & Tóth (2009).
  6. ^ Catlin (1979); Erdős & Fajtlowicz (1981).

References